Babylonian method #WSQ07

--Originally published at My Programming Course

For this WSQ I watched a video that JAVALIO posted: https://www.youtube.com/watch?v=9BvTRoXag0w

This method is for getting the square root of a number.

Src: https://github.com/YosefatJQ/TC201/blob/master/babylonian.java

WSQ 07

--Originally published at chozaoop

Also forgot this one, we also did this one as a team, same, we did the logic stuff and operations in a blank page and then wrote the code based on this.

Here’s a snip of the code:

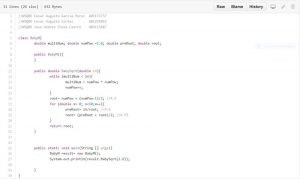
Kind of the same as the WSQ06, we initialized the variables from the beginning, no constructor and a single class that makes two loops to get the whole process done.

It was my fault to post this at the very end of the course but, well, some people procrastinates real hard sometimes.

Here’s the link to Cesar’s Github.

WSQ07 – Babylonian Method

--Originally published at finntc2016

This WSQ was easy. With my knowledge I gained doing WSQ06 and this explanation on how the Babylonian method works I was done soon.

Here you can find the corresponding repository:
https://github.com/finntec/wsq07.git

Old baby… a kid?

--Originally published at Juan Salvador Fernández Contreras

Pretty much the same as WSQ06, but with the babylonian method, so yeah.

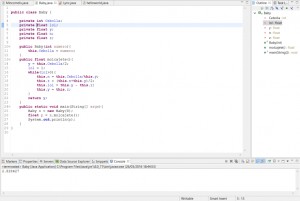
Still, both Gerardo and I had a lot of trouble getting it to work, turns out it was a simple problem of indentation, lol. At the same time a friend of mine from ISC showed me how he did “196” WSQ08, but I still preffer to find my own way of doing it, we’ll see how it goes.

And just for heck of it:

WSQ07 – Babylonian Method

--Originally published at JAVALIO

Cesar Cortez and Andres Choza also worked with me during the WSQ07, here we came with a little more of knowlegde about Java, but even though we still have dounts.

Babylonian Method is about finding the root of a number but in a different way, first we have to see the number given like for example, 19, then look for a x number that x^2 is the closest number we can approch to 19.

For example: 1×1 = 1, 2×2 =4, 3×3=9, 4×4=16, 5×5=25

So 19 is (4^2) and (5^2 ), so we can infer that the root of 19 is 4.### something because is between 4×4 and 5×5

For more information I recommend you to see this video:

Our code in Github: https://github.com/cesarau04/WSQ-Java/blob/master/wsq07.java

Image by vasse nicolas,antoine.

WSQ07-Babylonian Method

--Originally published at diegotc2016

Doing this wsq was more or less difficult for me because I’m still having problems with the syntaxis of Java. First I tried to “translate” my old code in Python to Java, but my program didn’t work, but I finally got the code right.

Here’s a video that helped me for this WSQ:

I tried to do the WSQ using this guy method but the console displayed an error

Here’s my code in Eclipse using as an input number 36:

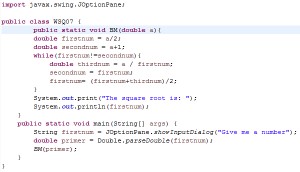
Here’s my code in Github:https://github.com/diegoalatorre/TC2016meromero/blob/master/WSQ07.java

Valentine’s day: Method not found

--Originally published at Social coding

I needed to finish my WSQs so I grab the coffee, my pc and some food and began the coding.
First, I need to say something to my pc because Valentine’s day. PC I love you more than Java. Ok, I know I am really bad at flirting and the computer is no exception.

Keep focus! You need to work, you need the PC to be proud. (This type of posts are what you got after not sleeping all weekend, thank you Tec!)
So here is the minimum common divisor, it was pretty easy and I did it with a friend to help him.

And here is the Babylonian, I am surprised. They were very intelligent or have a lot of free time, imagine what we can do without Tec having all our time. Joking, we love all the work…~~please don’t strike me with the entrepreneurial lightning~~

#WSQ07 Babylonian Method

--Originally published at Fernando Partida's Blog

It’s a tad bit late, and I can not think of a quirky title for this blog post so here’s the Babylonian method transferred into java.

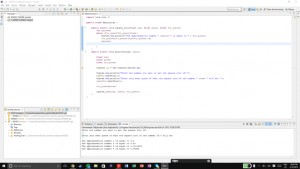
For this WSQ I used some of the methods from the past WSQ to obtain the user input. The program allows the user to input a number, and allows him to guess a possible solution, after running the input through the equation, the program will approximate the answer..after that it was just using a while loop and everything went swiftly.

hehehehehe it went Taylor Swift… (kill me)

Here’s the GitHub link.

#WSQ07

--Originally published at Jsph's Blog

The Babylonians had an accurate and simple method for finding the square roots of numbers. This method is also known as Heron’s method, after the Greek mathematician who lived in the first century AD. Indian mathematicians also used a similar method as early as 800 BC. The Babylonians are credited with having first invented this square root method, possibly as early as 1900 BC.

The Babylonian method for finding square roots involves dividing and averaging, over and over, to obtain a more accurate solution with each repeat of the process.

Last semester I did this program in Python but now it’s very different and more complex. However, I saw some codes of my classmates and did some research to achieve this wsq. It was not difficult but you need to think clearly how to use this method.

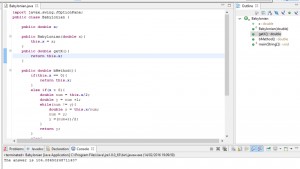
I use import javax.swing.JOptionPane;. This is a pane to ask an input to the user. This is located in the javax.swing library. The JOptionPane class allows you to have input boxes

I saw this video too:

and also I visited my new friend stackoverflow:

http://stackoverflow.com/questions/24092196/babylonian-algorithm-in-java

And the link of my code:

https://github.com/JsphSalazar/POO/blob/master/WSQ07

WSQ07 – Babylonian Method in JAVA

--Originally published at Alan TC201

This babylonian method was a little difficult, simply because compared to python, Java has a very weird syntax. I had to use a method of this person that I foun on the internet. (http://www.dreamincode.net/forums/topic/43600-babylonian-algorithm/)

Here is a link to understand Babylonian Method (https://www.deltacollege.edu/dept/basicmath/Babylonian.htm)