--Originally published at Hermes's Blog
Introducción y antecedentes
El método de bisección se utiliza para encontrar una raíz aproximada de una función, que se buscará dentro de un intervalo inicial [a, b], en el cual ocurre un cambio de signo en la función evaluada, es decir, f(a)f(b) < 0, por lo que el intervalo [a, b] debe contener un valor c, donde f(c) = 0. El teorema del valor intermedio para funciones continuas, que establece que si f es continua en [a, b] y si k es un número entre f(a) y f(b), entonces existe por lo menos un c ∈ (a, b) tal que f(c) = k.
Algoritmo
- Se eligen valores iniciales para a y b de tal forma que la función cambie de signo: f(a)f(b) < 0.
- Se bisecta el intervalo [a, b], calculando el punto intermedio con x = (a + b) / 2, este será la primera aproximación a la raíz.
- Se selecciona el sub-intervalo en el que la raíz se debe de encontrar:
- Si f(a)f(b) < 0, entonces la raíz se encuentra en (a, x), ahora b = x.
- Si f(a)f(b) > 0, entonces la raíz se encuentra en (x, b), ahora a = x.
- Este proceso se repite hasta encontrar el valor de la raíz o uno muy cercano a ella, es decir, cuando f(x) ≤ |ε|.
Requisitos previos
Para poder utilizar el método de bisección se debe saber de antemano un intervalo en donde la función contiene una raíz, además, la función debe ser continua en [a, b].
Diagrama de Flujo
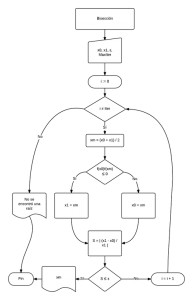
Criterio de detención
El método de bisección se detienen cuando se encuentra un valor c ∈ (a, b) tal que f(c) ≤ |ε|, donde ε es un valor próximo a cero. También se puede definir un número máximo de iteraciones para que el método se vea forzado a finalizar si no encuentra un valor que cumpla con los requisitos de terminación.
Código en c++
#include <cmath>
#define ITER 1000
#define MINERR 1E-15
typedef double (* vFunctionCall)(double x);
bool sameSign(double x, double y) {
return x * y >= 0;
}
double biseccion(vFunctionCall fun, double x0, double x1) {
double y0 = fun(x0);
double y1 = fun(x1);
if (y0 == 0) {
return x0;
} else if (y1 == 0) {
return x1;
}
int i = 0;
double x, y;
while (i < ITER) {
x = (x0 + x1) / 2;
y = fun(x);
if (abs(y) <= MINERR) {
return x;
}
if (sameSign(y, y0)) {
x0 = x;
y0 = y;
} else {
x1 = x;
y1 = y;
}
i++;
}
return x;
}
Pruebas:
| Función | Raices | [a, b] | Resultado |
|---|---|---|---|
| sin (x) + 2x – 1 | 0.335418 | [-10, 10] | 0.335418 |
| x^3 – 6 x^2 + 3 x + 10 | -1, 2, 5 | [-200, 600] | -1 |
| x ^ 4 – 2 x ^ 3 – 3 x ^ 2 + 4 * x + 4 | -1, 2 | [-2, 3] | f(a)f(b) < 0 (excepción) |
| x ^ 4 – 2 x ^ 3 – 3 x ^ 2 + 4 * x + 4 | -1, 2 | [-1, 2] | -1 |
| 1 / x^3 | y ≠ 0 | [-1, 1] | -1.86653e-301 |
| 1 / x^3 | No hay | [-999999999999999999, 999999999999999999] | -5e+17 |
Conclusiones
El método de bisección es el método más antiguo y elemental para determinar las raíces de una ecuación. Tiene limitantes, pues se necesita saber de antemano en que rango se encuentra la raíz. En las pruebas podemos observar que el algoritmo continua aún cuando f tiende a infinito en [a, b] hasta alcanzar el limite de iteraciones. El código pueden encontrarlo en github: https://github.com/hermesespinola/metodos_numericos/tree/master/bisection


