--Originally published at RAMGGV
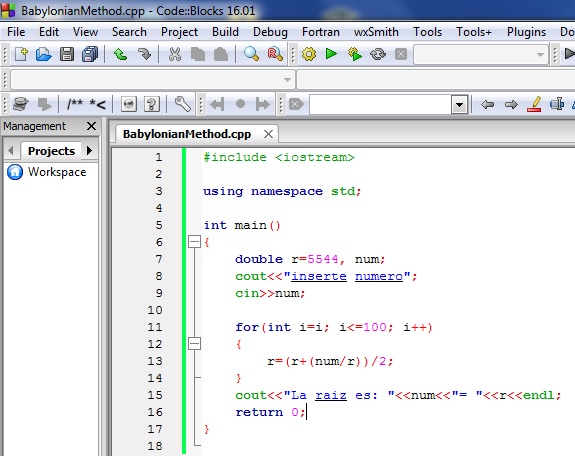
En este programa se tenia que sacar la raíz cuadrada de un numero, por medio del método babilonio.
--Originally published at RAMGGV
En este programa se tenia que sacar la raíz cuadrada de un numero, por medio del método babilonio.

--Originally published at Ken's Disciple 01
Guys here’s a video that shows exactly how to do this one, peace.
The code:
![]()
![]()
Code at GitHub
L.out
--Originally published at Loading…
In this assignment we had to:
write a function to calculate the square root of a number using the Babylonian method.
When I read it, I thought this would be a bit difficult, buuuuuuut it was pretty easy. First I investigated about this method, and this page is really good if you want to know about it. Also I found this flow diagram that helped me a lot:

So, the first thing that I did was add the <cmath> library. Then following the flow diagram I made my function. I established two variables, the b for the result, and dif for the diferencial. First we equate b with x, then made an operation in order to obtain the dif, if dif isn’t it less that 0.00001 the program prints the b, and made an other operation to give another value to b to get closer to the square root of x, and made the same until the condition is satisfy.

And here is how it works:

--Originally published at Programming course
So this was the assignment:
The function should receive a number and return floating point number. Obviously you should test your function, so create a main program that asks the user a value, calculates the square root and displays that.
And it was really simple after hearing Ken’s explanation and this article


--Originally published at blog de Horacio
The function should receive a number and return floating point number. Obviously you should test your function, so create a main program that asks the user a value, calculates the square root and displays that.
método babilonio:
El método babilónico de resolución de raíces cuadradas se centra en el hecho de que cada lado de un cuadrado es la raíz cuadrada del área. Fue usado durante muchos años para calcular raíces cuadradas a mano debido a su gran eficacia y rapidez. Para calcular una raíz, dibuje un rectángulo cuya área sea el número al que se le busca raíz y luego aproxime la base y la altura del rectángulo hasta formar o por lo menos aproximar un cuadrado.

code:
#include <iostream>
#include<cmath>
using namespace std;
float Bab(float x){
float b, diferencia;
b=x;
diferencia= abs(b- x/b);
while(diferencia > 0.00001){
std::cout <<b<< ‘\n’;
b= 0.5*(x/b+b);
diferencia= abs(b-x/b);
}
return b;
}
int main() {
float x;
std::cout << “dame el número :” << ‘\n’;
std::cout << “numero:” << ‘\n’;
std::cin >> x;
std::cout << “la raiz cuadrada de ” <<x<<“es: “<< Bab(x);
}
--Originally published at Solving problems with programming
What you need to do in this homework is calculate the square root using the babylonian method. To understand what is hte babylonian method i saw this video. It is simple, you use a simple formula. First of all you need an integer aproximation of the rootsquare with that you can do the babylonian mehtod x=aproximation z=number of the rootsquare you want to calculate rootsquare=(z/x+x)/2. With that formula you get the rootsquare with the babylonian mehtod. To have a more accurate result I use the result of the formula to repeat it as the aproximation again, and do it 30 times.
#include <iostream>
using namespace std;
double babylonian(int raiz, int numero){
double resultado,aprox,root;
root=raiz;
aprox=numero;
for (int i = 0; i < 30; i++) {
resultado=(aprox+(root/aprox))/2;
aprox=resultado;
}
return resultado;
}
main(){
int squareroot,aproximacion;
double resultado;
cout<< "Escribe la raíz que deseas sacar"<<endl;
cin>>squareroot;
cout<<endl<<"Escribe la aproximacion entera más cercana de esa raíz"<<endl;
cin>>aproximacion;
resultado=babylonian(squareroot, aproximacion);
cout<<"La raíz cuadrada es "<<resultado<<endl;
}
I need to improve this program and calculate the square root without the aproximation, but i don't know how, i will ask in the next class to my classmates --Originally published at Programming Path
Before the assignment, I didn’t know about the Babylonian Method to calculate the square root of a number. It was hard to understand, but with this tutorial (Eric Buffington) I could comprehend a bit.
Here is my code:
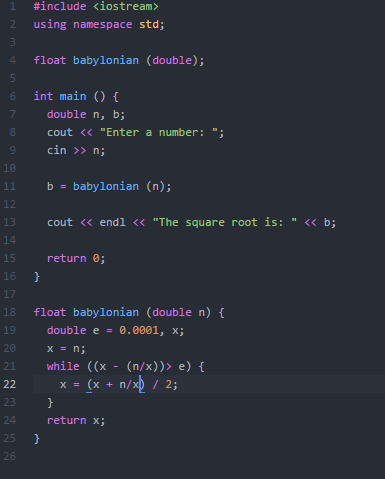
Thanks for reading.
--Originally published at OlafGC / Class #TC1017
Hi guys! It’s me again with a video of how to get the square root of a number using the old Babylonian method. The code and the link to the video are bellow:
#include <iostream>
#include <cmath>
using namespace std;
float babylonian_square(float x)
{
float ans, a=0;
ans=x/2;
do {
cout<<ans<<endl;
a=ans;
ans=(ans+x/ans)/2;
} while(abs (a-ans)>0.0001);
}
int main()
{
cout<<babylonian_square(2);
}
--Originally published at Adal´s Blog
--Originally published at Programming the city
Hey there guys!
Today I discovered another way to get the square root of a number; this way taught me that it is not neccesary to have a calculator to make different kind of operations and also I learned that we have problems every day but there are thousands of ways to solve them:).
The first advice for you to make this code is to include the cmath libray: this is because of the math operations we will need.
After that I added 6 variables which will help me to make the babylonian method. The first while is to know how many digits are in the number, the next part is when cont2 = cont-1; this is becaues after that I make the first operation of the babylonian method before the for, and as you can see, you have to make 1 less operation comparing to the number of digits of the number. For example if the number is 125348, it has 6 digits, so you have to make 5 operations of the babylonian method.
The las part, when I make the for, is to make the last 4 operations of the babylonian method.
And that’s it!

And the result is:

