--Originally published at Elu's Blog

As Ameer Fazal said in a video “recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem”. Note: that video is linked at the end of this post.

Here is an example of a recursive function:

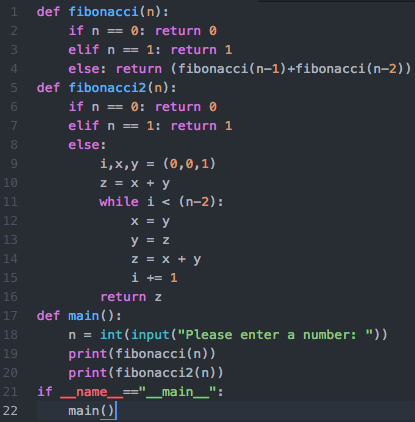
As we can see in the fibonacci function the fibonacci function is used. Wait what? Fibonacci-ception? It is very interesting and yet confusing. The way to understand it is by trying to use the function with a few examples. The first example, what happens if n = 0? It returns 0, ok easy. Second example, what happens if n = 1? It returns 1. Third example, what if n = 2? To answer that let’s go step by step:

1. Identify line 4: ‘else: return (fibonacci(n-1)+fibonacci(n-2))’. As we can see it will return the sum of ‘fibonacci(n-1)’ and ‘fibonacci(n-2)’.
2. ‘fibonacci(n-1)’ n = 2, so n – 1 = 2 – 1 = 1. And we already established that fibonacci(1) returns 1 so we got the first part of the sum.
3. ‘fibonacci(n-2)’ n = 2, so n – 2 = 2 – 2 = 0. And we already established that fibonacci(0) returns 0 so we got all parts of the sum.
4. At this moment, line 4 should hypothetically look like this: ‘else: return (1 + 0)’
5. ‘else: return (1)’ and the function overall returns 1.

Recursive functions look like tree when processed as we can see in the image below: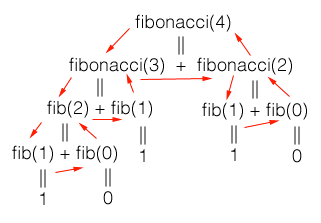

I know this is a hard topic to understand, especially if read and not heard or seen in another graphic way, so here is an alternative explanation:

Recursion : Python Tutorial #13 by Ameer Fazal