Simpson & Romberg

--Originally published at That Class Blog

Por: Arturo Fornés A01227071 y Miguel Montoya A01226045

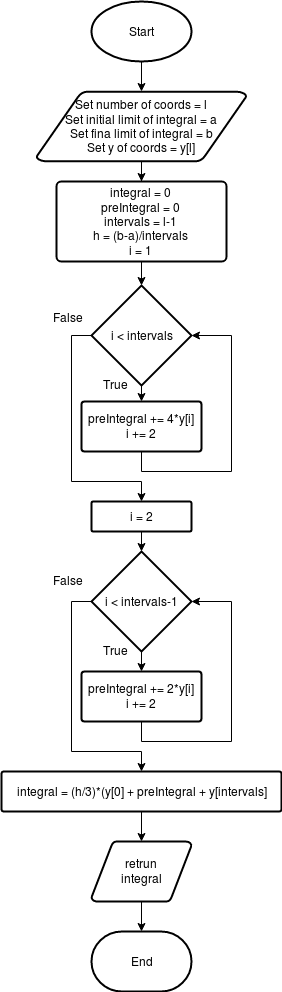
Nota: Tanto en el diagrama de flujo, como en el código y los ejemplos, utilizaremos el método de Simpson 1/3 múltiple.

Antecedentes

Hay varios métodos para calcular integrales definidas donde se hace una aproximación por cada intervalo, como Riemann desde la izquierda y derecha, o por método de trapecios. Existen dos métodos más complejos que obtienen una mejor aproximación, estos son los métodos de Simpson (Trataremos especialmente el de 1/3 múltiple) y el e Romberg.

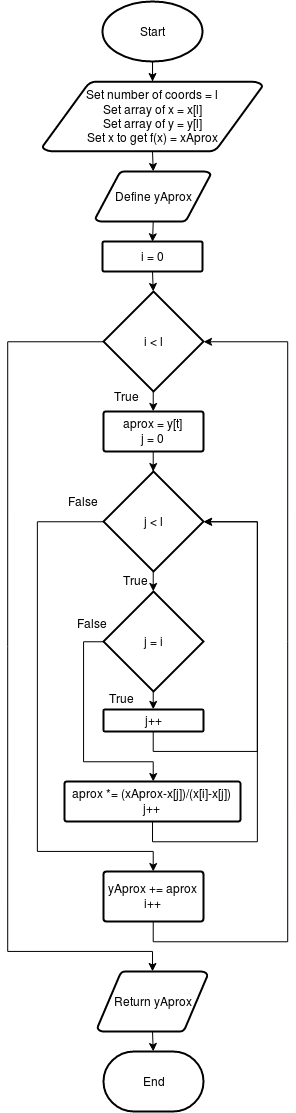
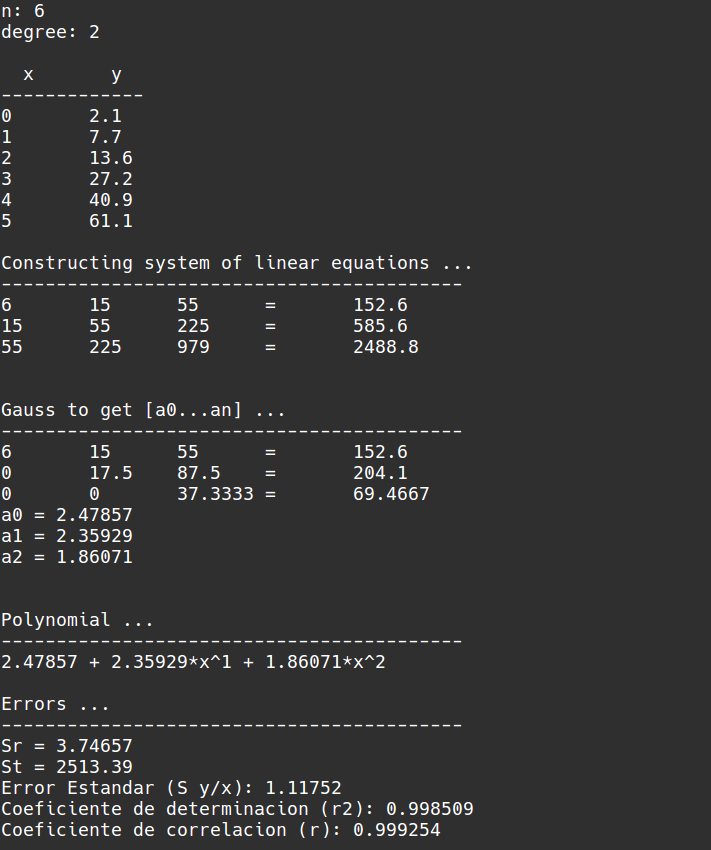
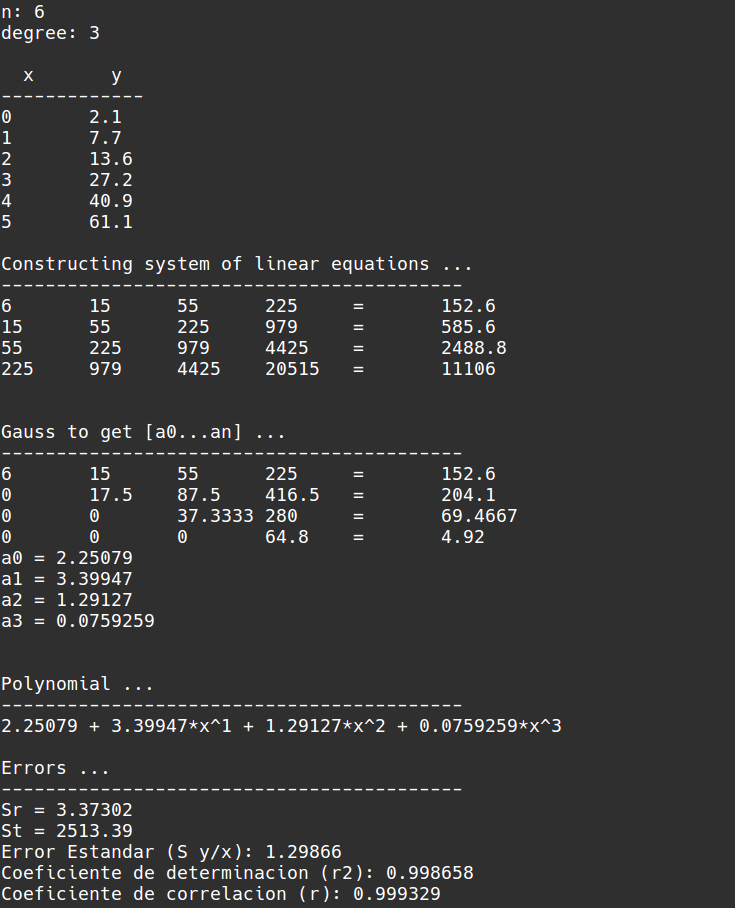
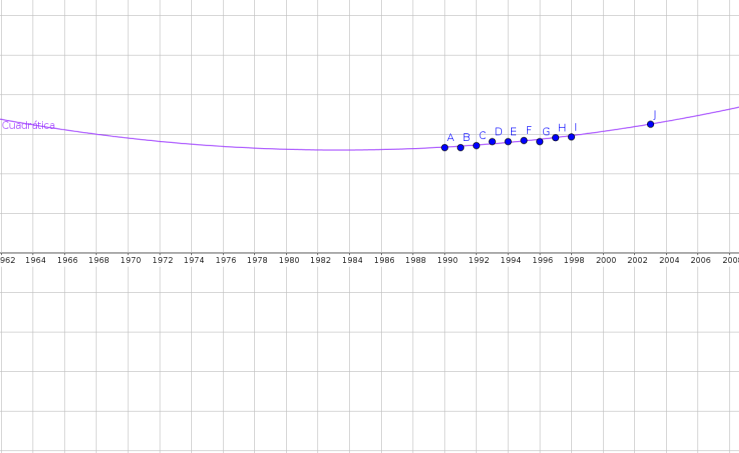
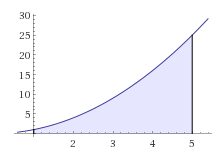
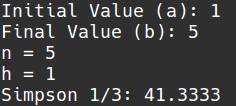
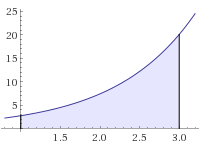
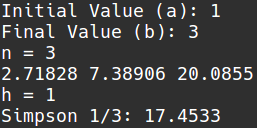
Simpson 1/3 está basado en la “interpolación cuadrática”, pues crea una función que pasa por todos los puntos dados e integra. La función es para dos intervalos continuos (Uniendo 3 puntos). La aplicación múltiple, es crear pares de intervalos para aplicar Simpson 1/3 a muchos puntos.

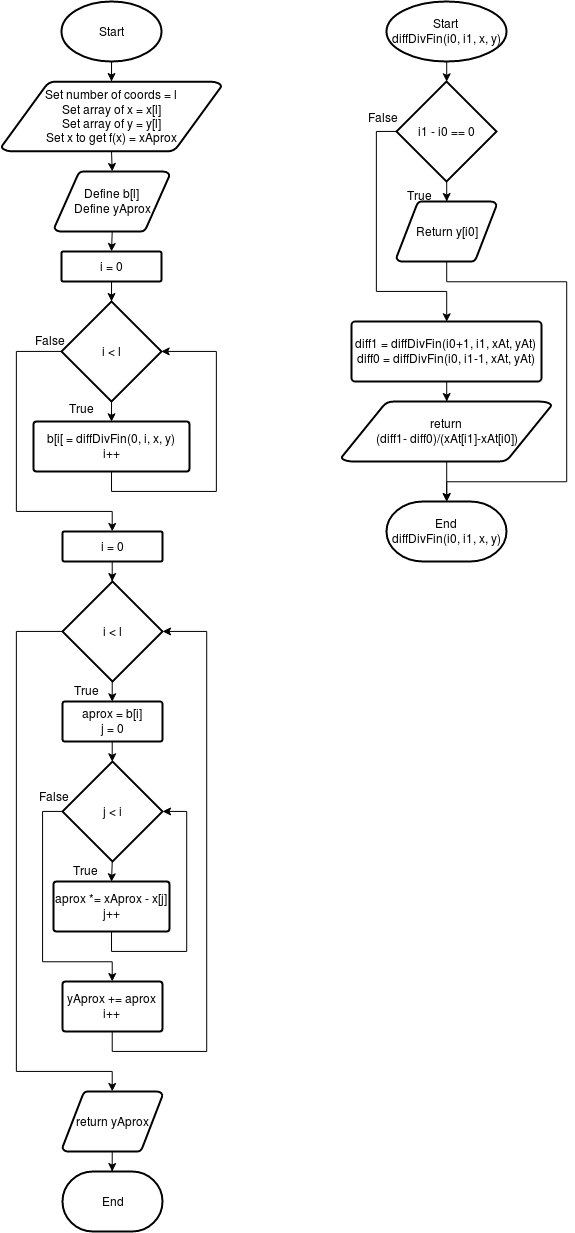
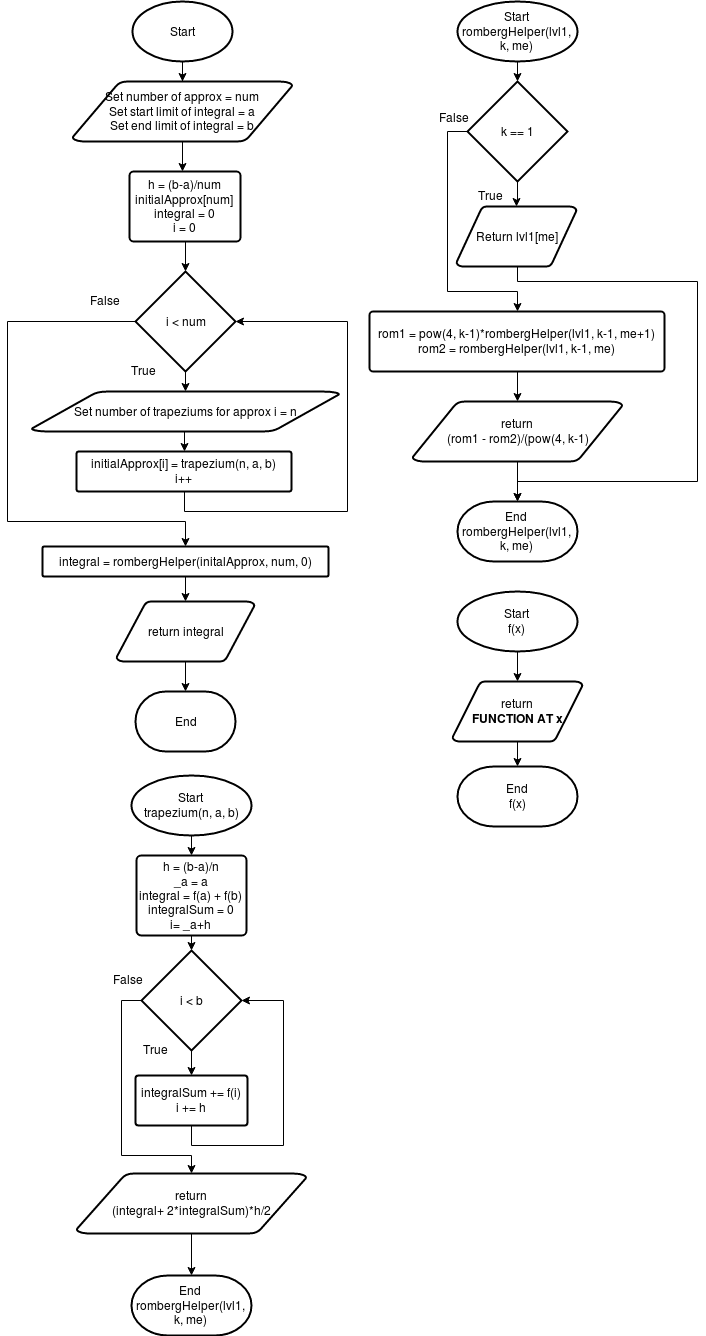
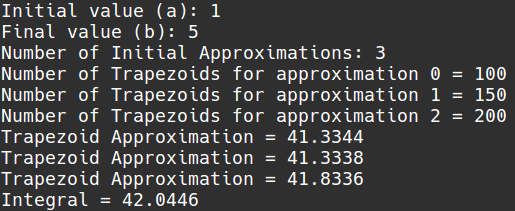
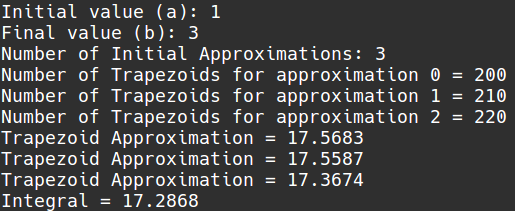
Romberg está basado en la integración por trapecios, y utiliza un método parecido a las diferencia divididas de Newton. Obtiene aproximaciones de integración con diferente número de trapecios para cada aproximación, y las mejora, hasta obtener un mejor resultado para la integral.

Justificación y propósito

Simpson 1/3 utiliza la siguiente función, para calcular la función perteneciente a los intervalos, antes de integrar.

P_{2}(x)=f(a){\frac {(x-m)(x-b)}{(a-m)(a-b)}}+f(m){\frac {(x-a)(x-b)}{(m-a)(m-b)}}+f(b){\frac {(x-a)(x-m)}{(b-a)(b-m)}}.

Debido a que siempre es la misma formula para obtener el polinomio, es fácil calcular la integral.

$I=\int _{a}^{b}f(x)\,dx$

Donde f(x) es el polinomio de Lagrange de grado dos. Podemos calcular una ecuación para cada intervalo, sin necesidad de calcular la integral de cada uno. $\int _{a}^{b}f(x)\,dx\approx {\frac {b-a}{6}}\left[f(a)+4f(m)+f(b)\right].$

Por otro lado, Romberg mejora el método de trapecios utilizando la siguiente formula

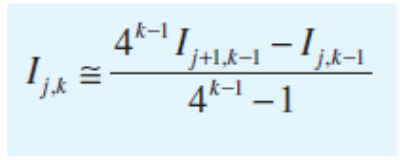
Donde se obtiene una integral mejorada, utilizando otras dos aproximaciones de trapecios, de menor nivel (Uno más exacto que el otro). Se denomina como aproximación más exacta a la que utilizo un mayor número de trapecios. Este método es recursivo, si obtienes x aproximaciones de un nivel mayor, todavía puedes obtener x-1 aproximaciones

Continue reading →

Interpolación de Newton y Lagrange

--Originally published at That Class Blog

Antecedentes

Ambas interpolaciones son métodos que permiten la creación de un polinomio de grado n-1, donde n es el número de datos que se tienen. Ambos métodos asumen que no existe ruido en sus mediciones de datos, es decir, que el polinomio generado por el método pasara por todas las coordenadas insertadas al método.

A menos que se conozca la función original (Lo cual es prácticamente imposible al aplicarlos en la vida real), no hay manera de calcular algún error.

Justificación y propósito

El propósito de ambos métodos es poder generar una función para la cual se puedan introducir todos los datos originales y obtener 0 error, pues la curva se va modelando punto a punto. Al obtener una función, se puede crear aproximaciones y estimaciones.
(En nuestros métodos, no proporcionamos al usuario la función, solamente el valor f(x) para la x deseada)

El método de Newton utiliza la formula de polinomios de Newton:

$N(x)=[y_{0}]+[y_{0},y_{1}](x-x_{0})+\cdots +[y_{0},\ldots ,y_{k}](x-x_{0})(x-x_{1})\cdots (x-x_{{k-1}}).$

El método de Larange obtiene una misma función, pero elimina por completo la necesidad de usar diferencias divididas:

$L(x):=\sum _{j=0}^{k}y_{j}\ell _{j}(x)$

donde

$\ell _{j}(x):=\prod _{\begin{smallmatrix}0\leq m\leq k\\m\neq j\end{smallmatrix}}{\frac {x-x_{m}}{x_{j}-x_{m}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}},$

Los polinomios de lagrange son más fáciles de computar, pues elimina la necesidad de recurrir a métodos de recursión,

Explicación gráfica de la interpolación

Estas gráficas representan dado un conjunto de puntos la interpolación de grado 1 a 4 de una funciócon la intención de obtener el valor de f(10), y cómo se ve reflejado esto en una gráfica.

Para la gráfica a) se hace una interpolación de grado 4, por lo que se utilizan los 5 puntos dados y se obtiene una función que cruce por estos puntos, luego se evalúa en x = 10.

Para

Continue reading →

Regresión Polinomial

--Originally published at That Class Blog

Antecedentes

Como ya fue explicado en el anterior post. La regresión (De cualquier tipo) es utilizada para generar una recta o curva que se ajusta a un diagrama de dispersión. Este diagrama contiene datos previamente capturados.

En el caso de regresión polinomial, el objetivo es crear una función que mejor se adapte a los datos introducidos. El grado de la función es especificado por el usuario.

Justificación y propósito

El propósito de todas las regresiones lineales es encontrar la relación de la variable dependiente con la independiente. Así realizar hipótesis, analizar tendencias y hacer estimaciones. En este caso se introducen términos polinomiales para realizar esta aproximación: a0 + a1*x + a2*x^2 + a3*x^3 + … + am*x^m

Al igual que anteriores métodos de regresión lineal, el error de regresión polinomial se mide a través del error estándar (Sy/x), coeficiente de determinación (r^2) y el coeficiente de correlación (r).