#TC1017 #QUIZ4
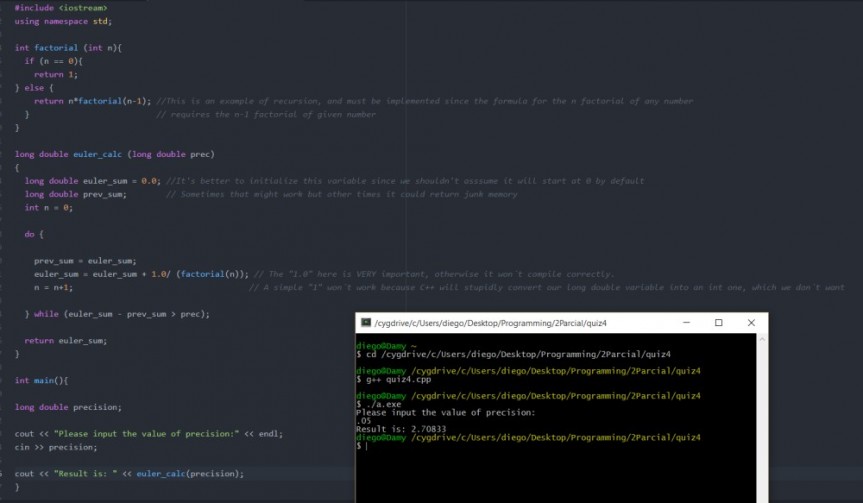
So this quiz was actually kinda challenging, it took me quite some time and a lot of questions to Ken to finally work it out. All noteworthy notes can be found on the picture below.
The factorial function was taken from one of the WSQs we did before, the tricky part was that C++ wasn´t giving me all decimals beacause of a disparity with the function’s types. Ken sorted that out😀
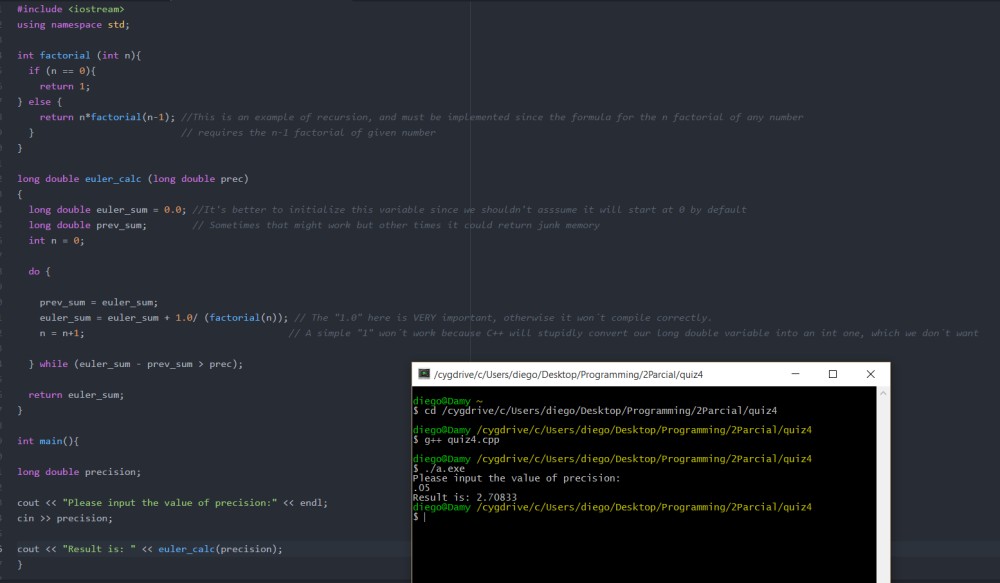
Source Code below [GitHub Link: https://github.com/diegodamy/Quiz4 ]
#include <iostream>
using namespace std;
int factorial (int n){
if (n == 0){
return 1;
} else {
return n*factorial(n-1); //This is an example of recursion, and must be implemented since the formula for the n factorial of any number
} // requires the n-1 factorial of given number
}
long double euler_calc (long double prec)
{
long double euler_sum = 0.0; //It’s better to initialize this variable since we shouldn’t asssume it will start at 0 by default
long double prev_sum; // Sometimes that might work but other times it could return junk memory
int n = 0;
do {
prev_sum = euler_sum;
euler_sum = euler_sum + 1.0/ (factorial(n)); // The “1.0” here is VERY important, otherwise it won´t compile correctly.
n = n+1; // A simple “1” won´t work because C++ will stupidly convert our long double variable into an int one, which we don´t want
} while (euler_sum – prev_sum > prec);
return euler_sum;
}
int main(){
long double precision;
cout << “Please input the value of precision:” << endl;
cin >> precision;
cout << “Result is: ” << euler_calc(precision);
}
—————————————————
Photo Credit: <a href=”https://www.flickr.com/photos/57329804@N00/9984539064/”>spanaut</a> via <a href=”http://compfight.com”>Compfight</a> <a href=”https://creativecommons.org/licenses/by-nc-sa/2.0/”>cc</a>
![]() Euler Aprox. by diegodamy is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Euler Aprox. by diegodamy is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.