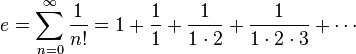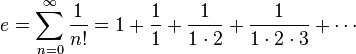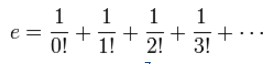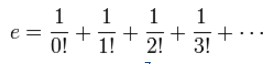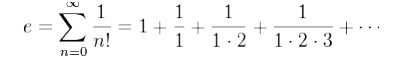
1+1/factorial.
La siguiente imagen explica los factoriales:
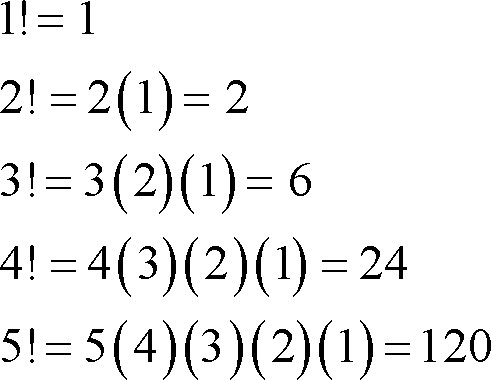
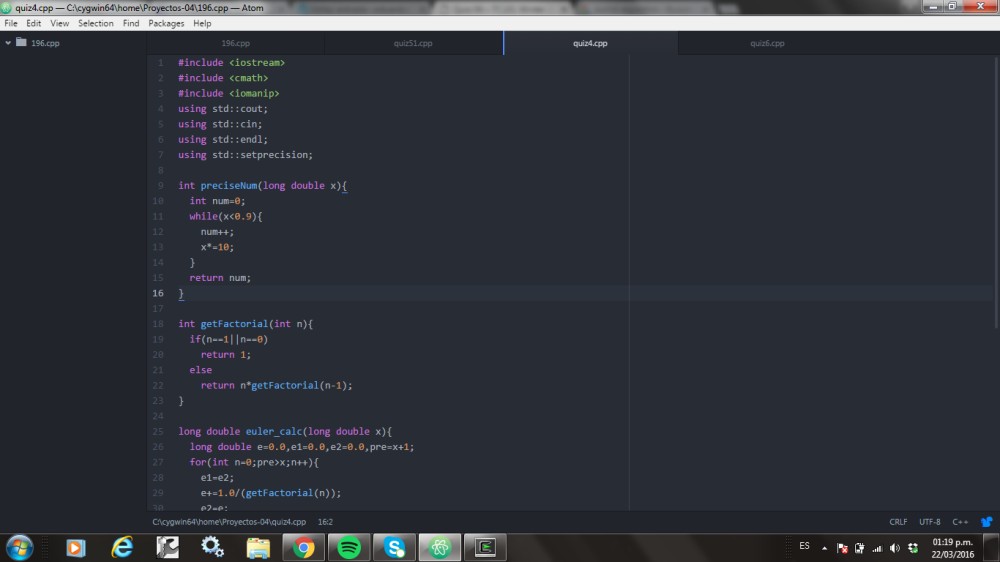
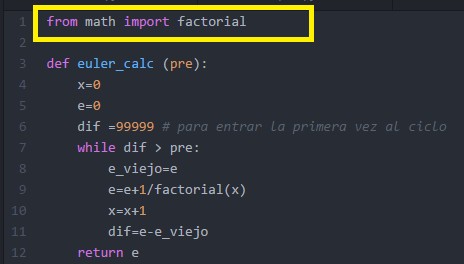
Para calcular el factorial de un número -WSQ09- los que lo hicieron sabrán :3 sino, en python ya existe una libreria de matematicas en la que calcula el factorial de un número.
math.factorial(n)
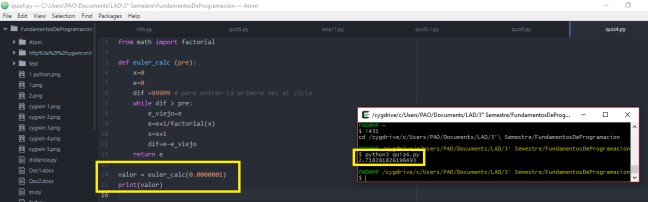
Mm. Como yo no tengo mis WSQ guardados, -acabo de formatear la lap- :l lo hice con esto. Oh, sorpresa, si lo tengo,
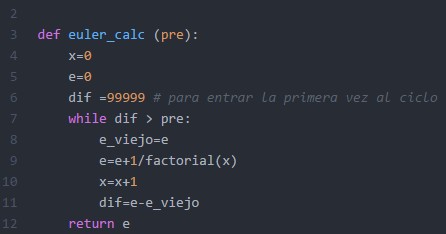
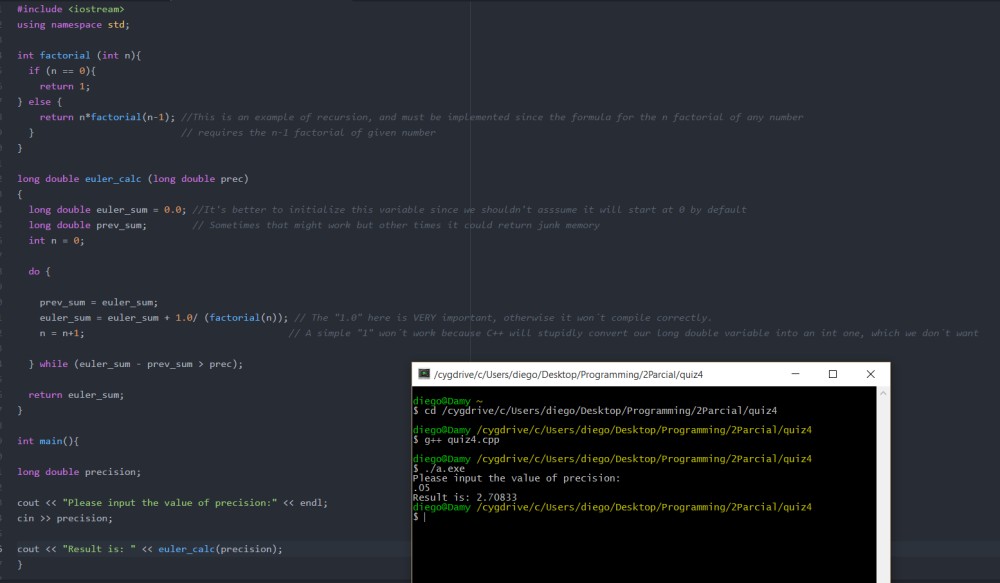
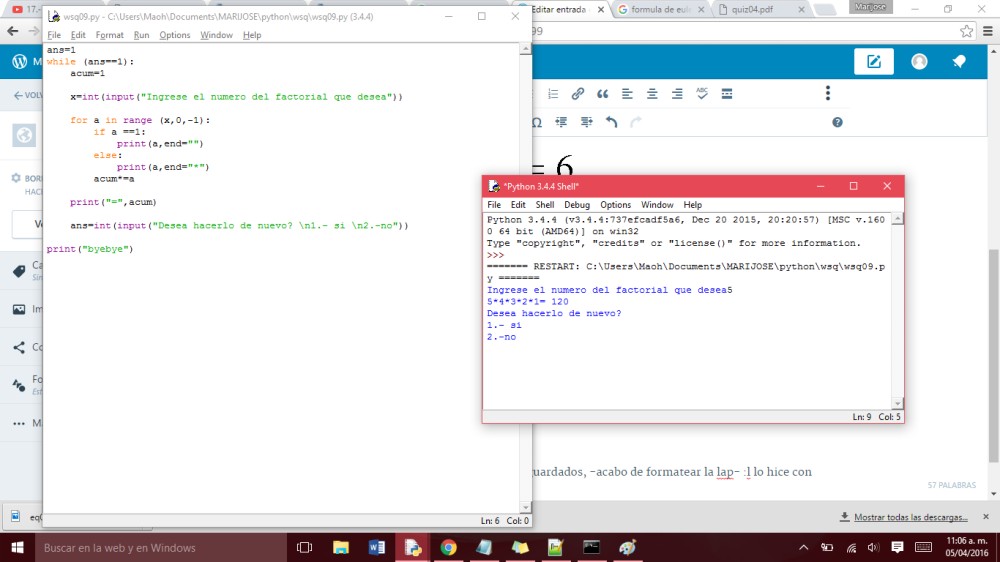 bueno, igual no lo tengo como una función, sólo quedaría meter todo eso dentro de una funcion (la parte donde calcula el factorial, sin las cosas fancy’s).
bueno, igual no lo tengo como una función, sólo quedaría meter todo eso dentro de una funcion (la parte donde calcula el factorial, sin las cosas fancy’s).
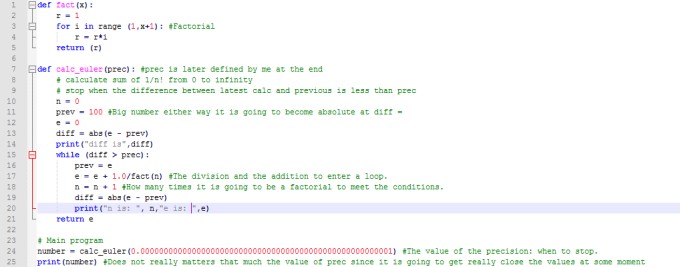
Y .. Ahora sí, teniendo lo que ocuparemos, va la explicación de la lógica.
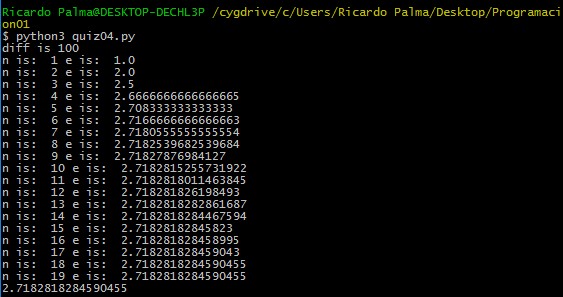
El número de Euler el valor máximo que puede dar es 2.71828 … Con esto sabremos si el programa está bien o no.
La formula es dada por suma de fracciones, en la cual, el numerador siempre va a ser 1 y el denominador es 1, 2, ,3… sucesivamente, pero es el factorial de ese número. Entonces… Si le pedimos al usuario que ingrese la precisión que quiere para calcular el número y nos da un.. 40. nuestra suma deberá ser 1+ 1/1! + 1/2! + 1/3! +…1/40! (el signo significa factorial. eso creo). El resultado será 2.71828…. El número de Euler- :3
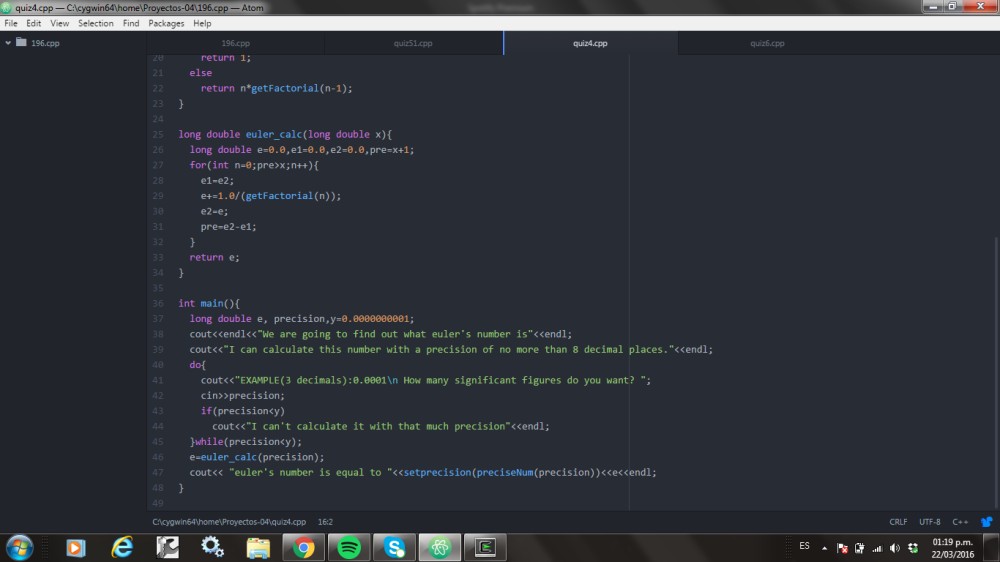
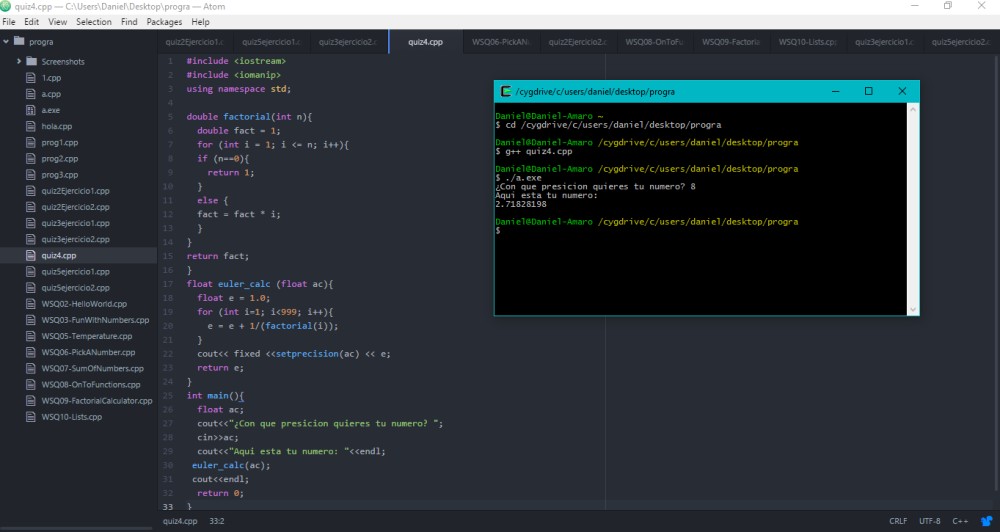
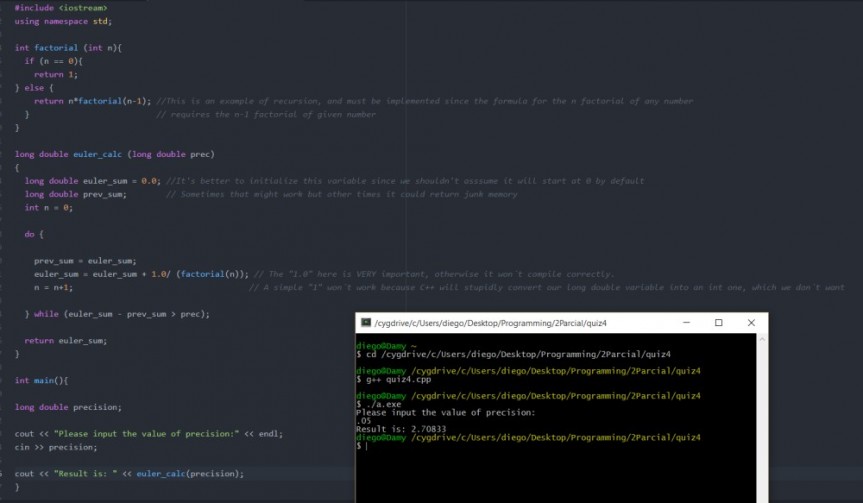
La repetición de algo nos lleva a un for, el cual se detendría hasta que llegue a n, que será l número ingresado por el usuario.
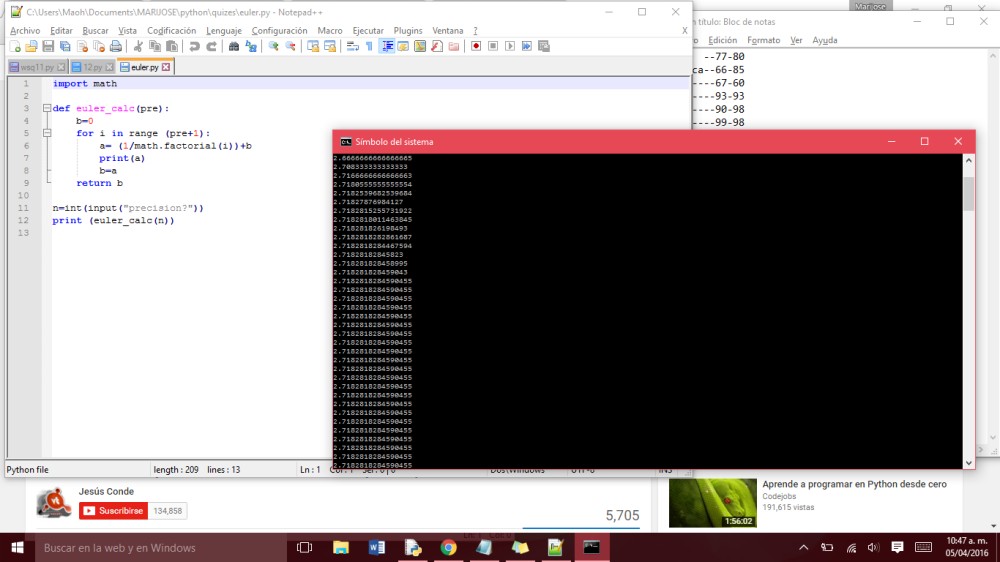
Y.. ahí esta desde el editor de Notepad++ -aunque no le guste a Ken- quizá no es tan bueno, y por bueno me refiero a interactivo.
For i in range (pre+1)… <- el pre + 1 sería el valor de n+1 , porque con los for comienza en 0. i será el valor que vaya aumentando+1 en cada vuelta, por lo tanto
Continue reading “Quiz 4/Euler” →


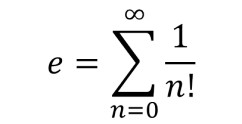
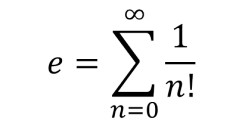
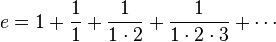


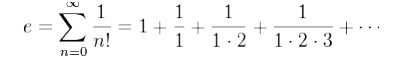
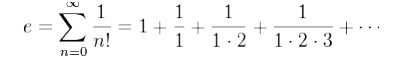
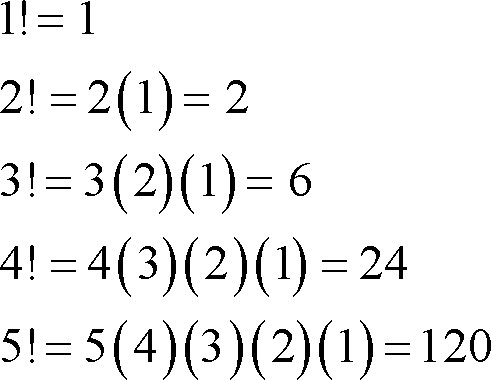
 bueno, igual no lo tengo como una función, sólo quedaría meter todo eso dentro de una funcion (la parte donde calcula el factorial, sin las cosas fancy’s).
bueno, igual no lo tengo como una función, sólo quedaría meter todo eso dentro de una funcion (la parte donde calcula el factorial, sin las cosas fancy’s).