In this quiz we had to make a program that tells you the greatest common divisor between two integer numbers. So the program asks for the biggest number and then the smallest.
For this we have to use the Euclid’s Algorithm: (Wikipedia obviously)
The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 147 = 252 − 105. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until one of the two numbers reaches zero. When that occurs, the other number (the one that is not zero) is the GCD of the original two numbers.
Here is a video, it´s in Spanish but explains this quite good:
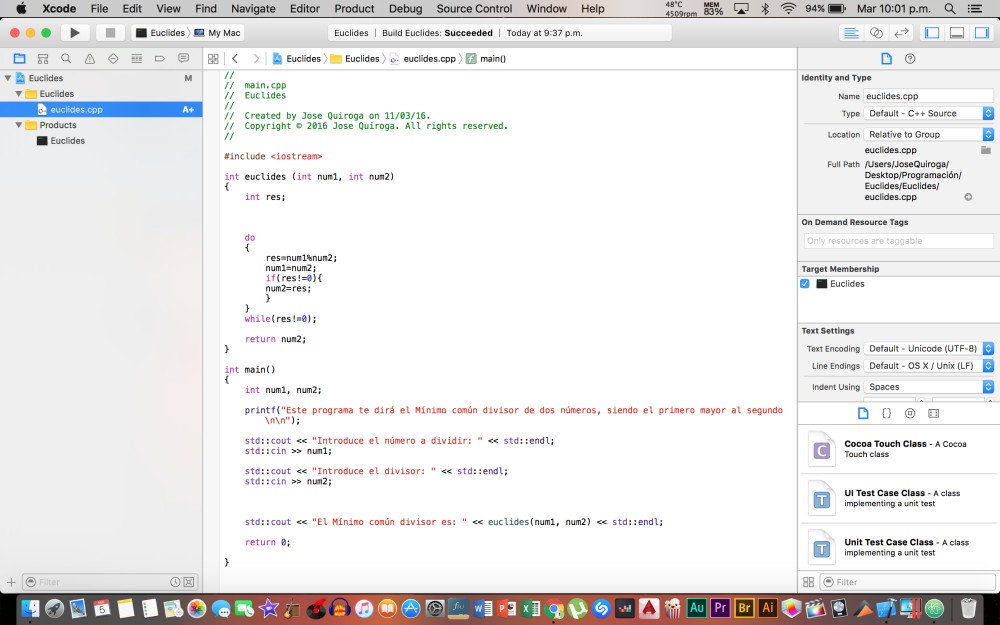
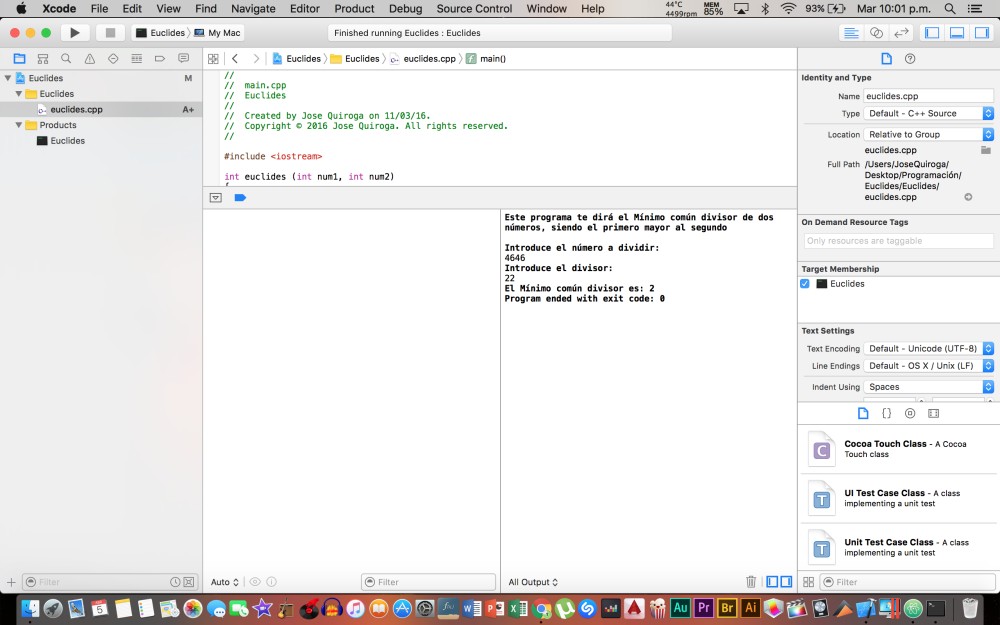
Thanks to Baruch who taught me how to make the loop.
Quiz 6 Euclides by josequirogablog is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
