--Originally published at richardctc201
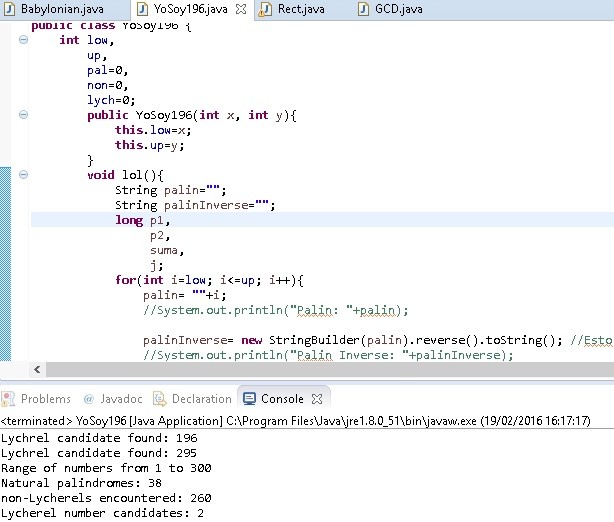
Finally I got to the final task of the first partial: the 196 activity. This activity consisted in creating a program to find possible Lychrel numbers in a specific range of data. Lychrel numbers are natural numbers that do not form palindromes after adding their inverse several times.
As usual, I asked for help to my new best friend Alex, and here is what he did: obviously (like in every previous programs) I created two classes, the main class and an additional class called ‘Range’. In my main class, I used a new thing (well, new for me) called JOptionPane to collect inputs given by the user. I had two of this so that the user could enter the lower and the upper limits of the range of numbers. In Range, I defined 5 variables: low, high, natural=0, non=0, and yes=0. I also created two methods: the first one called ‘rango’ (I’m Mexican so don’t nag me) that has two parameters a and b where a is defined as the lower bound, and b as the upper bound; the second one was the method where all the math calculations were made, this one was called ‘types’.
In main, I created one new object, and called method rango for it, passing the two inputs provided by the user as parameters. In types, I defines two variables (both strings): palin, and palinInverse, both variables were empty. I also defines 4 varibales as long: p1, p2, suma, and n. Finally I created a For loop with the condition that x=lower bound, and it iterate until x=upperbound. In the for loop, I made three conditions: one if that add one to my variable ‘natural’ if the number was a natural palindrome; another for loop to iterate thirty times to find Lychrel candidates, if there were palindromes in the way, it add one to ‘non’, and if not, it print an “Alert message” and add one to ‘yes’ meaning that it had found a Lychrel candidate.
I had a little problem with this code because first I defined my variables as float, but after just 10 iterations the numbers were incredibly huge, and the float variables couldn’t support it. So I had to change my variables to long, and then the program could successfully run.
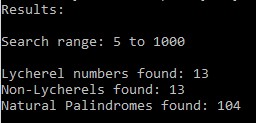
Here I leave screens of my program in Github:











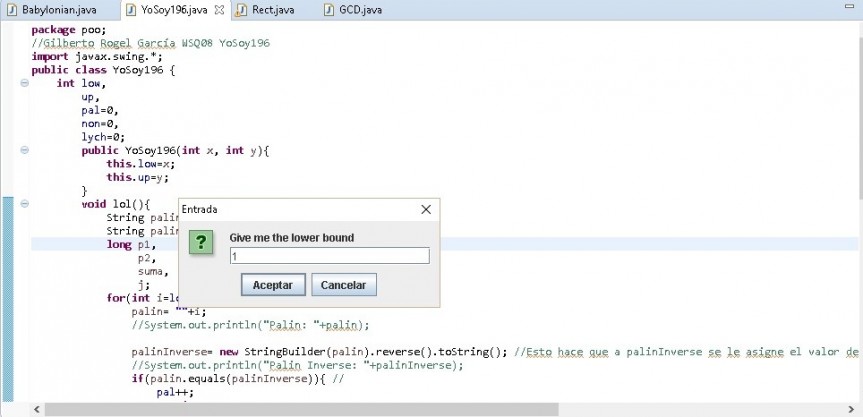
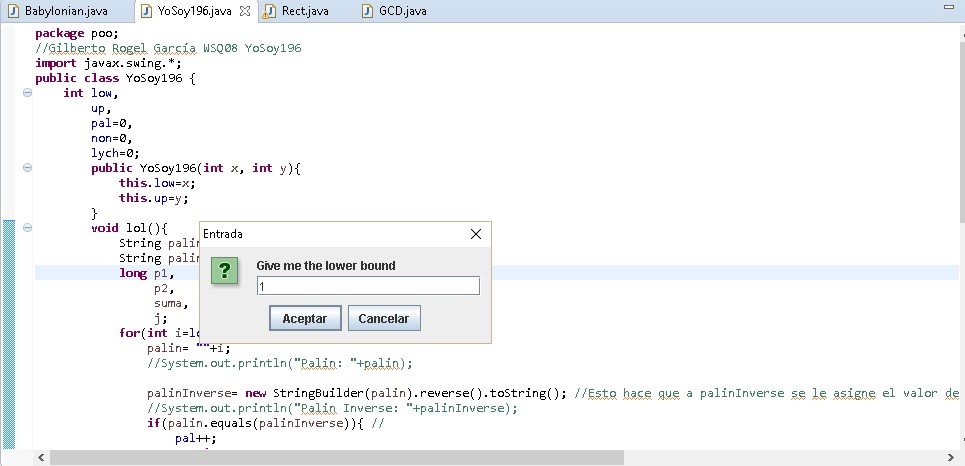 Lower Bound
Lower Bound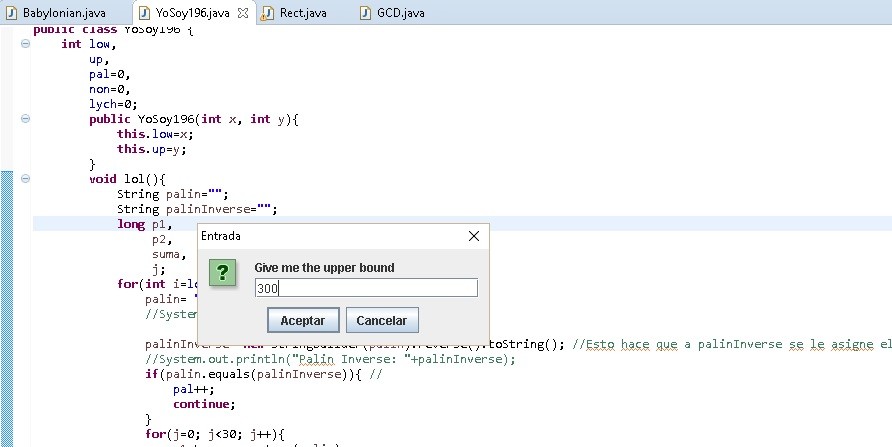 Upper Bound
Upper Bound