Simpson & Romberg

--Originally published at That Class Blog

Por: Arturo Fornés A01227071 y Miguel Montoya A01226045

Nota: Tanto en el diagrama de flujo, como en el código y los ejemplos, utilizaremos el método de Simpson 1/3 múltiple.

Antecedentes

Hay varios métodos para calcular integrales definidas donde se hace una aproximación por cada intervalo, como Riemann desde la izquierda y derecha, o por método de trapecios. Existen dos métodos más complejos que obtienen una mejor aproximación, estos son los métodos de Simpson (Trataremos especialmente el de 1/3 múltiple) y el e Romberg.

Simpson 1/3 está basado en la “interpolación cuadrática”, pues crea una función que pasa por todos los puntos dados e integra. La función es para dos intervalos continuos (Uniendo 3 puntos). La aplicación múltiple, es crear pares de intervalos para aplicar Simpson 1/3 a muchos puntos.

Romberg está basado en la integración por trapecios, y utiliza un método parecido a las diferencia divididas de Newton. Obtiene aproximaciones de integración con diferente número de trapecios para cada aproximación, y las mejora, hasta obtener un mejor resultado para la integral.

Justificación y propósito

Simpson 1/3 utiliza la siguiente función, para calcular la función perteneciente a los intervalos, antes de integrar.

{displaystyle P_{2}(x)=f(a){frac {(x-m)(x-b)}{(a-m)(a-b)}}+f(m){frac {(x-a)(x-b)}{(m-a)(m-b)}}+f(b){frac {(x-a)(x-m)}{(b-a)(b-m)}}.}

Debido a que siempre es la misma formula para obtener el polinomio, es fácil calcular la integral.

${displaystyle I=int _{a}^{b}f(x),dx}$

Donde f(x) es el polinomio de Lagrange de grado dos. Podemos calcular una ecuación para cada intervalo, sin necesidad de calcular la integral de cada uno. ${displaystyle int _{a}^{b}f(x),dxapprox {frac {b-a}{6}}left[f(a)+4f(m)+f(b)right].}$

Por otro lado, Romberg mejora el método de trapecios utilizando la siguiente formula

Donde se obtiene una integral mejorada, utilizando otras dos aproximaciones de trapecios, de menor nivel (Uno más exacto que el otro). Se denomina como aproximación más exacta a la que utilizo un mayor número de trapecios. Este método es recursivo, si obtienes x aproximaciones de un nivel mayor, todavía puedes obtener x-1 aproximaciones de nivel mayor.

Diagrama de flujo

Simpson 1/3 Múltiple.

Romberg.

Código en C++

Simpson 1/3 Múltiple: Github.

Romberg: Github.

Ejemplo comparativo

Para Simpson 1/3 múltiple, no se utiliza el método de trapecio para intervalos extra (En caso de que el número de intervalos sea impar, el último intervalo se integra con trapecios).

f (x) = x²

Se integra f(x) de 1 a 5:

Usando Simpson de 1/3 múltiple se obtiene una aproximación con una precisión de 0.00001:

Usando Romberg de 3 aproximaciones iniciales, usando aproximaciones iniciales de 100, 150 y 200 trapecios:

Romberg no fue preciso en este caso ya que este método fluctúa dependiendo de los valores de las aproximaciones por trapecios que se obtengan y qué tan diferentes sean estas entre sí.

f(x) = e^(x)

Se integra f(x) de 1 a 3:

Usando Simpson de 1/3 múltiple se obtuvo una aproximación con una precisión de 0.1:

Usando Romberg de 3 aproximaciones iniciales, usando aproximaciones iniciales de 100, 150 y 200 trapecios se obtuvo una aproximación a la integral definida con una precisión de 0.1:

En este caso ambos métodos dieron valores certeros, con el mismo grado de precisión.

Interpolación de Newton y Lagrange

--Originally published at That Class Blog

Antecedentes

Ambas interpolaciones son métodos que permiten la creación de un polinomio de grado n-1, donde n es el número de datos que se tienen. Ambos métodos asumen que no existe ruido en sus mediciones de datos, es decir, que el polinomio generado por el método pasara por todas las coordenadas insertadas al método.

A menos que se conozca la función original (Lo cual es prácticamente imposible al aplicarlos en la vida real), no hay manera de calcular algún error.

Justificación y propósito

El propósito de ambos métodos es poder generar una función para la cual se puedan introducir todos los datos originales y obtener 0 error, pues la curva se va modelando punto a punto. Al obtener una función, se puede crear aproximaciones y estimaciones.
(En nuestros métodos, no proporcionamos al usuario la función, solamente el valor f(x) para la x deseada)

El método de Newton utiliza la formula de polinomios de Newton:

$N(x)=[y_{0}]+[y_{0},y_{1}](x-x_{0})+cdots +[y_{0},ldots ,y_{k}](x-x_{0})(x-x_{1})cdots (x-x_{{k-1}}).$

El método de Larange obtiene una misma función, pero elimina por completo la necesidad de usar diferencias divididas:

$L(x):=sum _{j=0}^{k}y_{j}ell _{j}(x)$

donde

$ell _{j}(x):=prod _{begin{smallmatrix}0leq mleq k\mneq jend{smallmatrix}}{frac {x-x_{m}}{x_{j}-x_{m}}}={frac {(x-x_{0})}{(x_{j}-x_{0})}}cdots {frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}cdots {frac {(x-x_{k})}{(x_{j}-x_{k})}},$

Los polinomios de lagrange son más fáciles de computar, pues elimina la necesidad de recurrir a métodos de recursión,

Explicación gráfica de la interpolación

Estas gráficas representan dado un conjunto de puntos la interpolación de grado 1 a 4 de una funciócon la intención de obtener el valor de f(10), y cómo se ve reflejado esto en una gráfica.

Para la gráfica a) se hace una interpolación de grado 4, por lo que se utilizan los 5 puntos dados y se obtiene una función que cruce por estos puntos, luego se evalúa en x = 10.

Para la gráfica b) se hace una interpolación cúbica, por lo que sólo se utilizan los 4 puntos más cercanos a 10, se obtiene una función que cruce por estos puntos y se evalúa en x = 10.

Para la gráfica c) se hace una interpolación cuadrática, por lo que sólo se utilizan los 3 puntos más cercanos a 10, se obtiene una función cuadrática que cruce por estos puntos y se evalúa esa función en x = 10.

Para la gráfica d) se hace una interpolación lineal, por lo que sólo se utilizan los 2 puntos más cercanos a 10, se obtiene una función lineal que cruce por estos puntos y se evalúa esa función en x = 10.

Por estas gráficas se puede observar, también, la influencia que tiene el tamaño de la muestra para el resultado.

Diagrama de flujo

Newton

Lagrange

Código en C++

Newton (Github)
Lagrange (Github)

Ejemplos resueltos

A continuación se muestra los resultados de varias muestras resueltas por ambos métodos:

Con los siguientes puntos:

x, f(x) = (1, 0), (4, 1.386294), (6, 1.791759)

Se interpola usando estos datos para obtener una aproximación de f(5). Estos datos son muestras de la función f(x) = ln(x), por lo que ya conocemos el valor de f(5) = 1.61.

Con Polinomios de Interpolación de Newton se obtienen los valores para b0 … bn y aproximación siguientes:

Para Polinomios de Interpolación de Lagrange se obtienen los coeficientes de Lagrange y aproximación siguientes:

Con los siguientes puntos:

x, f(x) = (1, 1), (2, 0.5), (2.5, 0.4), (4, 0.25), (7, 0.14)

Se interpola usando estos datos para obtener una aproximación de f(3). Estos datos son muestras de la función f(x) = 1/x, por lo que ya conocemos el valor de f(3) = 0.33.

Con Polinomios de Interpolación de Newton se obtienen los valores para b0 … bn y aproximación siguientes:

Para Polinomios de Interpolación de Lagrange se obtienen los coeficientes de Lagrange y aproximación siguientes:

Regresión Polinomial

--Originally published at That Class Blog

Antecedentes

Como ya fue explicado en el anterior post. La regresión (De cualquier tipo) es utilizada para generar una recta o curva que se ajusta a un diagrama de dispersión. Este diagrama contiene datos previamente capturados.

En el caso de regresión polinomial, el objetivo es crear una función que mejor se adapte a los datos introducidos. El grado de la función es especificado por el usuario.

Justificación y propósito

El propósito de todas las regresiones lineales es encontrar la relación de la variable dependiente con la independiente. Así realizar hipótesis, analizar tendencias y hacer estimaciones. En este caso se introducen términos polinomiales para realizar esta aproximación: a0 + a1*x + a2*x^2 + a3*x^3 + … + am*x^m

Al igual que anteriores métodos de regresión lineal, el error de regresión polinomial se mide a través del error estándar (Sy/x), coeficiente de determinación (r^2) y el coeficiente de correlación (r).

Diagrama de flujo

Código en C++

Link a Github.

Ejemplos resueltos con gráficos y cuantificación del error

Regresión Lineal

--Originally published at Hermes's Blog

Antecedentes

El análisis de regresión es una técnica de modelado predictivo que investiga la
relación entre una variable dependiente y una variable independiente.
Es una herramienta importante en modelado y análisis de datos. Tratamos de
ajustar una curva o línea a la nube de datos de tal manera que las diferencias
entre las distancias de la nube de datos a la curva o línea sea mínima.
La regresión lineal es un modelo matemático usado para aproximar la relación de
dependencia entre una variable dependiente y variables independientes.
Hay innumerables formas de regresión, cada una tiene sus condiciones y
situaciones especificas donde aplican mejor que otras.

Justificación y propósito

Como mencioné anteriormente, el análisis de regresión estima la relación entre
dos o más variables. Los beneficios de usar regresión son:

Indica la relación significativa entre variable dependiente e independiente.
Indica la fuerza de impacto de multiples variables independientes en una
variable dependiente.

Fundamento matemático con gráficos

La regresión lineal se representa con una ecuación de la forma Y = a + b*X + e,
donde a es la intercepción, b es la pendiente de la linea y e es un termino de error.
Esta ecuación se puede utilizar para predecir el valor de la variable dependiente
basado en la(s) variable(s) predictoras.

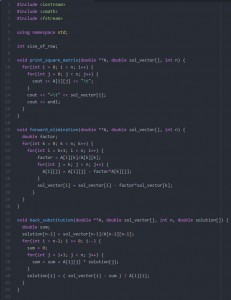
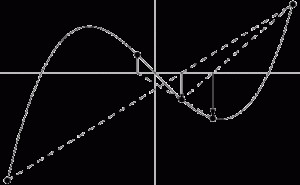
Para obtener la linea que mejor se ajusta a los datos (es decir, obtener a y b),
podemos usar el método de los mínimos cuadrados. Es el método más común usado
para ajustar una linea de regresión. Este calcula la linea a partir de los datos
observados minimizando la suma de los cuadrados de las desviaciones verticales
desde cada punto a la linea, debido a que las desviaciones están elevadas al
cuadrado, no se cancelan valores positivos y negativos cuando son sumadas.

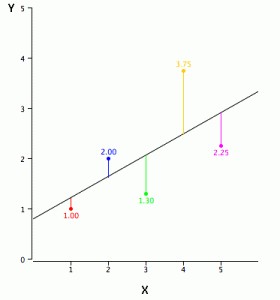
Podemos aplicar regresión lineal a cualquier nube de datos pero hay que
considerar que podría haber otro modelo predictivo que se ajuste mejor.
Además es importante notar que la regresión lineal es sensible a Outliers,
estos son, puntos que introducen ruido en nuestros datos debido a que no se
ajustan bien al modelo e introducen mucho error, modificando la aproximación.

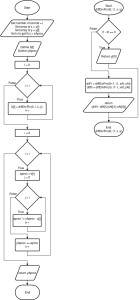
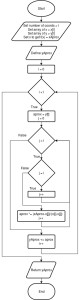
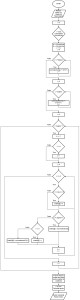
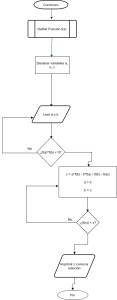
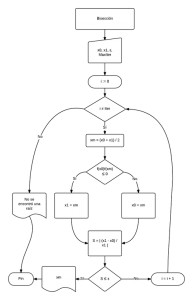
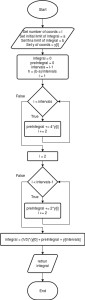
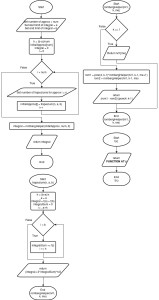
Diagrama de flujo

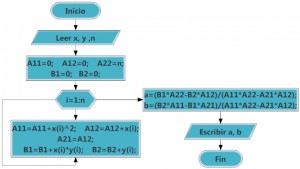
Ejemplos resueltos con gráficos y cuantificación del error

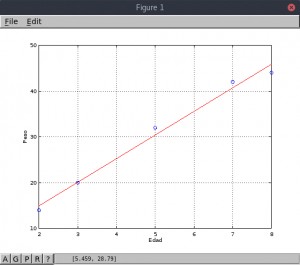
Cinco niños de 2, 3, 5, 7 y 8 años de edad pesan, respectivamente, 14, 20, 32, 42 y 44 kilos.

Edad	Peso
2	14
3	20
5	32
7	42
8	44

Standard error: 1.69161

Determination coefficient: 0.987722

Correlation coefficient: 0.993842

Equation: Y = 4.630769 + 5.153846 * X

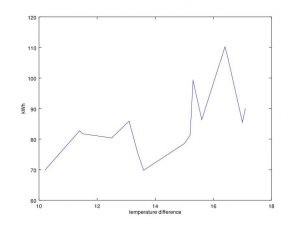
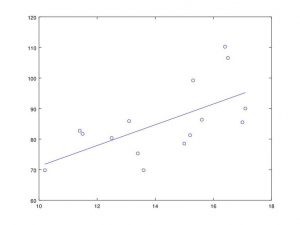
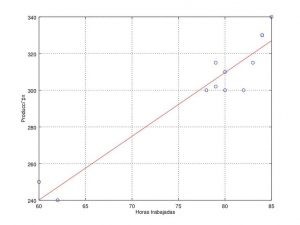
2. A partir de los siguientes datos referentes a horas trabajadas en un taller (X), y a unidades producidas (Y), determinar la recta de regresión de Y sobre X, el coeficiente de correlación lineal e interpretarlo.

Horas	Producción
80	300
79	302
83	315
84	330
78	300
60	250
82	300
85	340
79	315
84	330
80	310
62	240

Standard error: 9.46644

Determination coefficient: 0.910105

Correlation coefficient: 0.953994

Equation: Y_guess = 31.741135 + 3.473404 * X

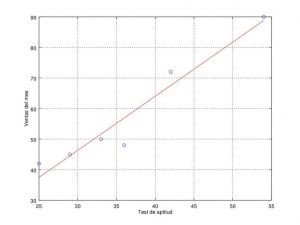
3. La tabla siguiente nos da las notas del test de aptitud (X) dadas a seis dependientes a prueba y ventas del primer mes de prueba (Y) en cientos de euros.

Test	Ventas del mes
25	42
42	72
33	50
54	90
29	45
36	48

Standard error: 5.57802

Determination coefficient: 0.931195

Correlation coefficient: 0.964984

Equation: Y_guess = -6.780155 + 1.770233 * X

Linealización de modelos no lineales

Algunas veces la regresión lineal puede ser usada en relaciones que no son
inherentemente lineales, después de aplicar una transformación.

Regresión exponencial

Consideramos el siguiente modelo exponencial: y = aexp(b x).

Aplicando el logaritmo natural a ambos lados de la ecuación tenemos la siguiente
ecuación equivalente: ln(y) = ln(a) + b * x.

Esta ecuación tiene la forma de un modelo de regresión lineal: y’ = a’ + b * x

Regresión potencial

Otro modelo de regresión no lineal es el modelo de regresión potencial, que se basa en la siguiente ecuación: y = a * x ^ b

Aplicando logaritmo a ambos lados de la ecuación, tenemos:
log(y) = log(a) + b * log(x)

Esta ecuación tiene la forma de un modelo de regresión lineal: y’ = a’ + b * x’

Ejemplos

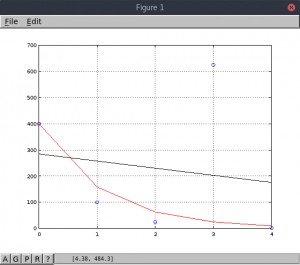
Con estos datos podemos apreciar en la gráfica de abajo que el modelo exponencial
(en rojo) se ajusta mucho mejor a los datos que el modelo lineal (en negro).
Cabe destacar que las regresiones están siendo afectadas por el Outlier que está
en (3, 625).

X	Y
0	400
1	100
2	25
3	625
4	1.5625

Equation: Y_guess = exp(5.991465) * exp(-0.925777 * X)

Standard error: 348.836

Determination coefficient: -0.233174

Correlation coefficient: 0.482881

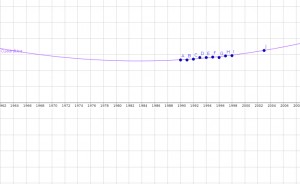
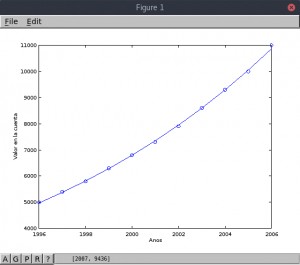
En este segundo caso el modelo que mejor se acerca es también el exponencial,
ajustandose casi perfectamente a los datos.

X	Y
1996	5000
1997	5400
1998	5800
1999	6300
2000	6800
2001	7300
2002	7900
2003	8600
2004	9300
2005	10000
2006	11000

Equation: Y_guess = exp(-147.463576) exp(0.078144 X)

Standard error: 54.522

Determination coefficient: 0.999313

Correlation coefficient: 0.999656

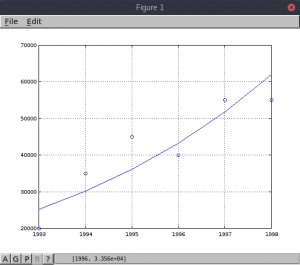
En este tercer ejemplo el modelo exponencial se ajusta bien a los datos, a pesar
de que estos esten más dispersos.

X	Y
1993	20000
1994	35000
1995	45000
1996	40000
1997	55000
1998	55000

Equation: Y_guess = exp(-348.387392) * exp(0.179891 * X)

Standard error: 7048.29

Determination coefficient: 0.775211

Correlation coefficient: 0.880461

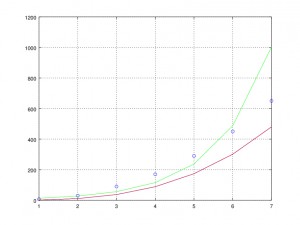
En este cuarto ejemplo no es muy claro cuál de los dos modelos se ajusta mejor,
sería necesario tener más datos para poder dar una respuesta acertada.

X	Y
1	7
2	30
3	90
4	170
5	290
6	450
7	650

Con regresión potencial (rojo):

Equation: Y_guess = 10^0.127025 * X.^3.022645

Standard error: 121.887

Determination coefficient: 0.781831

Correlation coefficient: 0.884212

Con regresión exponencial (verde):

Equation: Y_guess = exp(1.865637) * exp(0.720691 * X)

Standard error: 162.971

Determination coefficient: 0.609981

Correlation coefficient: 0.781013

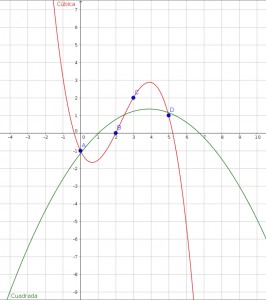
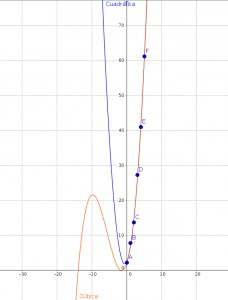
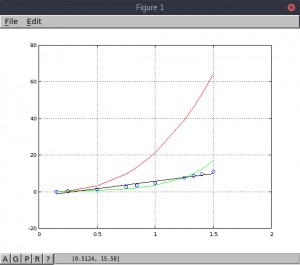
En este quinto ejemplo los datos están mucho menos dispersos y casi podría ajustarse
una linea de regresión (en negro). el modelo potencial (en rojo) no es para nada adecuado.
Parace que el modelo exponencial (en verde) se alejariía cada vez más al predecir valores
para x > 1.5.

X	Y
1	7
2	30
3	90
4	170
5	290
6	450
7	650

Modelo exponencial (verde)

Equation: Y_guess = exp(1.865637) exp(0.720691 X)

Standard error: 162.971

Determination coefficient: 0.609981

Correlation coefficient: 0.781013

Modelo potencial (rojo)

Equation: Y_guess = 10^0.127025 * X.^3.022645

Standard error: 121.887

Determination coefficient: 0.781831

Correlation coefficient: 0.884212

Modelo lineal (negro)

Standard error: 71.6407

Determination coefficient: 0.92463

Correlation coefficient: 0.961577

Equation: Y_guess = -183.142857 + 106.035714 * X

Regresión lineal

--Originally published at Hermes's Blog

En quince casas de la ciudad se observó durante un período de tiempo la diferencia de temperatura promedio (en grados centígrados) entre la temperatura en la calle y la temperatura en casa, y el consumo de electricidad diario en kWh

Graficas de datos

Podemos percibir que entre más sube la diferencia de temperatura entre la casa y la calle
suele haber más consumo de energía eléctrica.

Aplique regresión lineal y obtenga la función lineal que se ajusta a estas mediciones.

corriendo el siguiente código con los datos proporcionados obtenemos los resuldatos de a1 = 3.39553 a0 = 37.1618, lo que quiere decir que el y = 37.1618 + 3.39553 * x es un modelo lineal que se ajusta apropiadamente a estos datos.

Error estándar de la estimación

El error estandar está definido por la desviación estandar entre la raíz del numero
de datos: std_dev / sqrt(n). Así pues, encontramos que el error estandar de la
estimación es de 509.583.

Coeficiente de correlación

El coeficiente de correlación de Pearson es una medida de relación lineal entre dos variables aleatorias
cuantitativas y lo podemos utilizar como índice para medir el grado de relación de dos variables.

Encontramos que el coeficiente de correlación en los datos es de -6.81036e+31.

Grafica de la regresión lineal

Conclusiones

Comparación de métodos para encontrar raíces

--Originally published at Hermes's Blog

Método	Tipo	Requisitos	Riesgos	Convergencia	Ventajas	Desventajas	Tolerancia al error	Tipo de raíces que encuentra	Cuántas raíces encuentra
Bisección	cerrado	Se debe saber de antemano un intervalo en donde la función contiene una raíz, además, la función debe ser continua en un intervalo de busqueda [a, b]	Ninguno si se cumple con los requisitos previos	Si se cumple con los requisitos previos se garantiza su convergencia	Es mucho más seguro que otros métodos en el sentido de que garantiza la convergencia	Es menos eficiente que el método de Newton-Raphson	Se usa el error absoluto	Reales	Una
Newton-Raphson	abierto	Sólo requiere un valor de inicio x y la derivada de la función	A veces diverge o se aleja de la raíz verdadera a medida que se avanza en el cálculo.	Con base en la serie de Taylor, tenemos que la velocidad de la convergencia está expresada por E_{i+1} = O(E_{i^2}); de esta manera el error debe de ser proporcional al cuadrado del error anterior	Cuando sí converge, lo hacen mucho más rápido que los métodos cerrados	en el caso de raíces múltiples e inclusive en raíces simples se nos pueden llegar a presentar algunas dificultades, como por ejemplo convergencia lenta o casos en el que un punto de inflexión* se encuentra en la vecindad de una raíz	Se usa el error iterativo	Reales	Una
Secante	abierto	necesitamos conocer las dos aproximaciones anteriores	la convergencia no se asegura si la primera aproximación a la raíz no es lo suficientemente cercana a ella, ni tampoco se asegura cuando la raíz es múltiple	el orden de convergencia en un punto cercano a la solución es φ (número áureo). En caso de que la aproximación inicial sea demasiado lejana o la raíz no sea simple, este método no asegura la convergencia	No se necesita el calculo de la derivada	Su velocidad de convergencia es menor al de otros métodos abiertos	Se usa el error iterativo	Reales	Una
Bairstow	Abierto	La función debe ser un polinomio.	Los polinomios de grado muy alto o impar con multiplicidad total a una raíz pueden hacer que el método falle o que el resultado no sea tan exacto.	Si se utiliza Newton-Raphson para calcular las raíces, es cuadrática.	Puede encontrar todas las raíces de una función si se trata de un polinomio.	No funciona con funciones trigonométricas o exponenciales.	Gran tolerancia al error, no se indetermina con tanta facilidad como otros métodos, y en casos de polinomios de muy alto grado, da resultados aceptables.	Reales y complejas	Dependiendo de la implementación, puede llegar a calcular desde dos hasta n raíces que tenga el polinomio

Método de la secante

--Originally published at Hermes's Blog

Método Secante

El método de la secante es un algoritmo para encontrar la raíz de una función que se asume que es aproximadamente lineal en la región de interés. Cada aproximación se toma como el punto donde la linea secante corta el eje x.

Método secante

En qué consiste

Se basa en obtener la ecuación de la recta que pasa por los puntos (x_i-1, f(x_m.1)) y (x_i, f(x_i)). A dicha recta se le llama secante por cortar la gráfica de la función. Posteriormente se escoge como siguiente elemento de la relación de recurrencia x_i+1, la intersección de la recta secante con el eje de las abscisas obteniendo la fórumula y un nuevo valor. A continuación continuamos con este proceso, hasta llegar a un nivel de precisión suficientemente alto (una diferencia suficientemente pequeña entre x_n y x_n-1).

Se basa en la fórmula de Newton-Raphson, pero evita el cálculo de la derivada usando la siguiente aproximación:

f'(x) ≈ (f(x_i-1) – f(x_i)) / (x_i-1 – x_i)

Sustituyendo en la fórmula de Newton-Raphson obtenemos:

x_i+1 = x_i – f(x_i)/f'(x_i) ≈ x_i – (f(x_i) * (x_i-1 – x_i) / f(x_i-1) – f(x_i))

Requisitos previos

Es importante notar que para poder calcular la siguiente aproximación x_i+1 necesitamos conocer las dos aproximaciones anteriores, x_i y x_i-1.

Diagrama de flujo

Diagrama de flujo del método secante

Criterio de detención del método

El método de la secante se detendrá cuando el error iterativo (ε) sea lo suficientemente pequeño, para lograr un nivel de precisión lo suficientemente aceptable.

Cabe destacar que el orden de convergencia en un punto cercano a la solución es φ (número áureo). En caso de que la aproximación inicial sea demasiado lejana o la raíz no sea simple, este método no asegura la convergencia.

Código fuente


#include <cmath>
 
#ifndef MINERR
#define MINERR 1E-6
#endif
 
typedef double (* vFunctionCall)(double x);
 
double secante(vFunctionCall fun, double x1, double x2) {
  double x0;
  int i = 0;
  do {
    x0=x1;
    x1=x2;
    x2 = x1 - (x1-x0) * fun(x1) / (fun(x1) - fun(x0));
    // if (fun(x2) == 0) { 
    //   return x2; 
    // } 
    i++;
  } while ( fabs (x1-x2) > MINERR );
 
  fprintf(stderr, "Iteraciones: %dn", i);
  fprintf(stderr, "Error: %fn", fabs(x1 - x2));
  return x2;
}

Pruebas y resultados

Casos de exito:

f(x)	x_1	x_2	iteraciones	Resultado
x ^ 2 – 4	1	5	9	2
x ^ 2 – 4	-100	-101	15	-2
atan(x)	1	8	9	0
cos(3 * x) – x	-1.39174	-1.39174	11	-0.979367

Casos frontera:

f(x)	x_1	x_2	iteraciones	Resultado
x ^ (1/3)	1	0	1	0
x ^ 3 – x – 11	-10	5	10	2.373650

Casos de falla:

f(x)	x_1	x_2	iteraciones	Resultado
x ^ (1/3)	-20	20	1	-nan
x ^ 3 – x – 11	-100	100	132415	-nan

Conclusiones

El método de la secante es un método abierto que podemos aplicar cuando la función f(x) es demasiado compleja como para obtener su derivada (que se usaría en el método de Newton-Raphson). Es decir: si f(x) es tan compleja que es dispendioso obtener f'(x), es mejor usar el método de la secante. Empero, su velocidad de convergencia es menor que la de otros métodos como Newton-Raphson, y además dicha convergencia no se asegura si la primera aproximación a la raíz no es lo suficientemente cercana a ella, ni tampoco se asegura cuando la raíz es múltiple, en dados casos nos arriesgamos a que el método no converja y no podamos encontrar la raíz.

Método de Bisección

--Originally published at Hermes's Blog

Introducción y antecedentes

El método de bisección se utiliza para encontrar una raíz aproximada de una función, que se buscará dentro de un intervalo inicial [a, b], en el cual ocurre un cambio de signo en la función evaluada, es decir, f(a)f(b) < 0, por lo que el intervalo [a, b] debe contener un valor c, donde f(c) = 0. El teorema del valor intermedio para funciones continuas, que establece que si f es continua en [a, b] y si k es un número entre f(a) y f(b), entonces existe por lo menos un c ∈ (a, b) tal que f(c) = k.

Algoritmo

Se eligen valores iniciales para a y b de tal forma que la función cambie de signo: f(a)f(b) < 0.
Se bisecta el intervalo [a, b], calculando el punto intermedio con x = (a + b) / 2, este será la primera aproximación a la raíz.
Se selecciona el sub-intervalo en el que la raíz se debe de encontrar:
- Si f(a)f(b) < 0, entonces la raíz se encuentra en (a, x), ahora b = x.
- Si f(a)f(b) > 0, entonces la raíz se encuentra en (x, b), ahora a = x.
Este proceso se repite hasta encontrar el valor de la raíz o uno muy cercano a ella, es decir, cuando f(x) ≤ |ε|.

Requisitos previos

Para poder utilizar el método de bisección se debe saber de antemano un intervalo en donde la función contiene una raíz, además, la función debe ser continua en [a, b].

Diagrama de Flujo

Criterio de detención

El método de bisección se detienen cuando se encuentra un valor c ∈ (a, b) tal que f(c) ≤ |ε|, donde ε es un valor próximo a cero. También se puede definir un número máximo de iteraciones para que el método se vea forzado a finalizar si no encuentra un valor que cumpla con los requisitos de terminación.

Código en c++


#include <cmath>
 
#define ITER 1000
#define MINERR 1E-15
 
typedef double (* vFunctionCall)(double x);
 
bool sameSign(double x, double y) {
  return x * y >= 0;
}
 
double biseccion(vFunctionCall fun, double x0, double x1) {
  double y0 = fun(x0);
  double y1 = fun(x1);
 
  if (y0 == 0) {
    return x0;
  } else if (y1 == 0) {
    return x1;
  }
 
  int i = 0;
  double x, y;
  while (i < ITER) {
    x = (x0 + x1) / 2;
    y = fun(x);
 
    if (abs(y) <= MINERR) {
      return x;
    }
 
    if (sameSign(y, y0)) {
      x0 = x;
      y0 = y;
    } else {
      x1 = x;
      y1 = y;
    }
    i++;
  }
 
  return x;
}

Pruebas:

Función	Raices	[a, b]	Resultado
sin (x) + 2x – 1	0.335418	[-10, 10]	0.335418
x^3 – 6 x^2 + 3 x + 10	-1, 2, 5	[-200, 600]	-1
x ^ 4 – 2 x ^ 3 – 3 x ^ 2 + 4 * x + 4	-1, 2	[-2, 3]	f(a)f(b) < 0 (excepción)
x ^ 4 – 2 x ^ 3 – 3 x ^ 2 + 4 * x + 4	-1, 2	[-1, 2]	-1
1 / x^3	y ≠ 0	[-1, 1]	-1.86653e-301
1 / x^3	No hay	[-999999999999999999, 999999999999999999]	-5e+17

Conclusiones

El método de bisección es el método más antiguo y elemental para determinar las raíces de una ecuación. Tiene limitantes, pues se necesita saber de antemano en que rango se encuentra la raíz. En las pruebas podemos observar que el algoritmo continua aún cuando f tiende a infinito en [a, b] hasta alcanzar el limite de iteraciones. El código pueden encontrarlo en github: https://github.com/hermesespinola/metodos_numericos/tree/master/bisection